Introduction

科學在不知道原理前一切就像魔術一樣，但是在解析背後的原理以後，看似不可能的都會馬上變得理所當然。今天來分享一個大家都曾經看到也困惑的現象，逆行滾動的雙錐，一個違反直覺的科學魔術。最後還有更令人訝異精彩的震盪雙錐，大家也別錯過！(如果已經看過逆行雙錐的，可以跳過直接看震盪雙錐！)

那在開始分析之前，我們先看看這樣的影片吧

逆行雙錐

可以看到原本的柱體沿著載台由高處往低處滾動，然而雙錐卻反其道而行，由低處往高處滾動。看似不合理的行為，但其實這件事情的關鍵就在於滾體的質心位置！如果仔細的你透過觀察，會發現雙錐在''看似''逆行而上的過程中，中間錐體的部分似乎有往下陷下去的趨勢。那這個原因就是錐體會逆行而上的關鍵證據！然而這只是我們定性的觀察和推測，接下來我們要用點數學把這樣的結果給描述出來，就更加清楚明朗了！

那現在我們先不考慮雙錐放在載台不同位置的狀況，而暫時先不考慮載台傾斜的狀態。 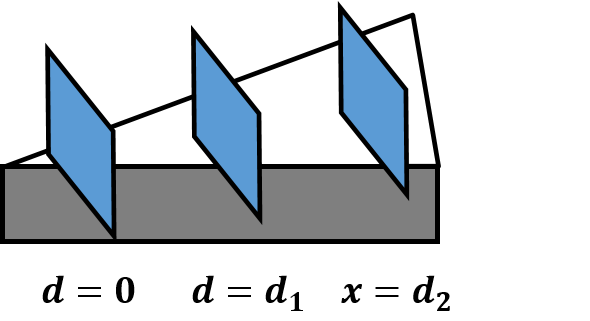當雙錐放在載台不同位置時，我們可以很清楚得看到其質心高度隨著不同地方的變化。因為載台在不同位置開口的大小不同，導致雙錐陷下去的深度也不同，也表示雙錐離地面的質心位置是載台位置的一個函數。那從側視圖，我們可以看到更清楚的結果： 可以發現其實雙錐的質心隨著$d=0$ 至 $d=d_2$ 時其質心是往下降的，也因此雙錐在這個三角開口的載台上本來就會自然地由$0$往$d_2$的地方移動了。

有趣的事情是，如果我們現在讓載台有一個傾斜的角度使得$d_2$處的載台較高，但是這個高度差還不至於超過雙錐在$d_2$所下降的高度，整體系統處在$d_2$處得重力位能還是較低。因此雙錐還是會往$d_2$滾動，儘管視覺上看起來雙錐是沿著載台往高處移動的有趣錯覺呢！

現在已經定性瞭解了這樣的系統以後，我們來進一步用數學來解釋和證明這樣的現象所需的條件。首先我們先給定系統一些數學代號吧！ Fig.1

因為我們知道雙錐可以假設成一個函數 $f(x)$ 繞著$x$軸旋轉所形成的錐體。

因此我們只要知道雙錐從中點$O$延水平延伸和載台相交的距離 $L(d)$ ，我們就可以得知所對應錐體質心和載台相切的距離$\overline{\mathrm{O}\mathrm{P}}$ 為$f\left(x=L\left(d\right)\right)$

已知載台會剛好與雙錐相切因此我們有 \[x=L\left(d\right)\] 而整體錐體重心距離地面的高度可以由幾何關係得到質心距離地面的高度為 \[C\left(d\right)=h+f(x)\] 此時我們是不考慮載台傾傾斜的狀況，若是載台傾斜了，則$h$就會隨著$d$的位置而改變，也就是$d$的函數，因此我們可以把雙錐重心高度隨著載台位置改變寫成 \[\mathrm{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ }C\left(d\right)=h\left(d\right)+f\left(x=L\left(d\right)\right)\] 接下來我們只要把$h(d)$以及$f(x)$的關係式給寫出來即可以計算

那首先先處理最簡單的$h(d)$好了，他的關係是也十分的單純，因為傾斜只是單純的線性的關係。 因此我們可以把高度隨距離$d$的變化寫成 \[h\left(d\right)=dsin\phi \] 接下來我們來處理我們的$f\left(x=L\left(d\right)\right)$，那先處理$L(d)$關係式的部分 從幾何關係馬上就看到$L$和$d$的關係式也是很簡單的一個三角函數關係而已 \[L\left(d\right)=dtan\alpha \] 最後我們在想看看我們的$f(x)$是怎麼樣的函數了，可以發現我們的雙錐只不過是繞著一條線性的方程式所旋轉的錐體而已 因此最後我們帶回我們的錐體質心高度的公式 \[C\left(d\right)=h\left(d\right)+f\left(x=L\left(d\right)\right)\] \[C\left(d\right)=dsin\phi +f\left(\boldsymbol{dtan}\boldsymbol{\alpha }\right)\] \[C\left(d\right)=dsin\phi +f\left(\boldsymbol{dtan}\boldsymbol{\alpha }\right)\] 那其實可以發現對於我們在fig1中的錐體，原點的半徑$R$就是方程式的截距、斜率就是$-tan\theta $ \[C\left(d\right)=dsin\phi +\left(-tan\theta \times dtan\alpha +R\right)\] 整理得到 \[C\left(d\right)=dsin\phi -dtan\theta tan\alpha +R\] 若是要讓雙錐往高處滾動則隨著$d$大，$C(d)$要變小 因此我們有 \[C^{'}\left(d\right)=sin\phi -tan\theta tan\alpha < 0\] 也就是你們常看到的 \[sin\phi < tan\theta tan\alpha \] 的條件了

因此只又錐體的幾何形狀和載台的開角以及傾角滿足這樣的關係，錐體就會產生往高處逆行的錯覺了！

震盪雙錐

現在證明完了逆行雙錐的運動情形以後，還有個更有趣的現象，稱作震盪雙錐。和逆行雙錐不同的地方是這個雙錐不只會逆行往上，還會來會的載台中來會滾動！由於這個雙錐有趣的設計，讓整個系統又變得更加有意思了！可以看看以下的影片，可以看到這個錐體的邊緣是設計成曲線的樣子，這個形體又被稱作$pseudosphere\ $



這個pseudosphere can ascend or oscillate back and forth,太神奇了 馬上吸引奇異鳥目光，為何會這樣呢? 那其實這也滿簡單的只要把我們剛剛所用的錐體$f(x)$公式稍微改寫一下你就懂了

若是我們考慮這樣的錐體，他是以 \[y=\frac{1}{x}\] 繞$x$軸所形成的旋轉體

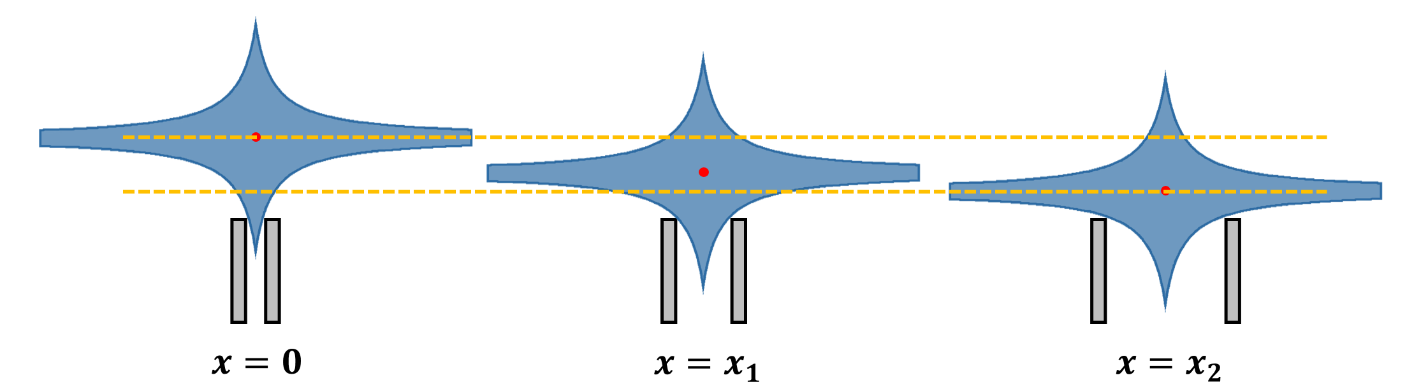當他放置在載台上時，你會發現他一樣隨隨著距離，他的重心也會下降，就跟剛剛的狀況一樣，但是有趣的事情要馬上出現了 如果我們假設我們的錐體他的函數是 \[y=\frac{1}{ax-b}\] 帶入我們剛剛的公式以後 \[C\left(d\right)=dsin\phi +f\left(dtan\alpha \right)\] \[\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =dsin\phi +\frac{1}{datan\alpha -b}\] 這個形式跟剛剛的雙錐有點不同

由於這個方程式比較難用解析解來解釋，所以我用數學軟體把這位能的方程式給畫出來，來分析位能隨著距離變化的狀況。

綠色是$y=xsin\phi $

藍色是 $y=\frac{1}{xatan\alpha -b}$

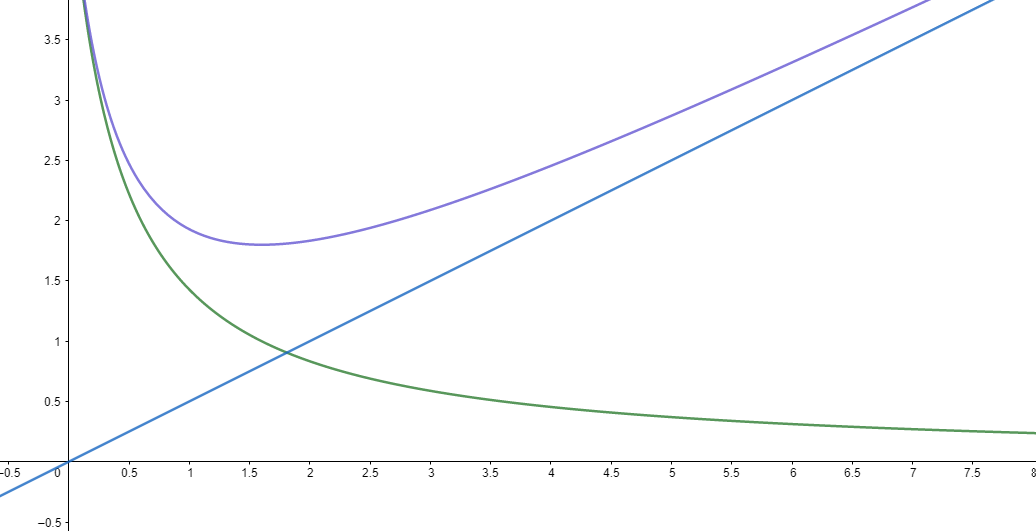紫色是$y=xsin\phi +\frac{1}{xatan\alpha -b}$ (也就是兩個的加總) 從圖表我們可以發現有個位能低點，也因此如果我們從$x=0$處釋放雙錐，他自然會往右邊移動到達最低位能處，但同時又保有動能衝到更右邊後失去動能以後，又往左邊移動，也就會在這個位能井當中來回的擺盪，也就是前面所說跟各位所看到的現象'' oscillate back and forth''

同樣的我也把一般雙錐的圖畫出來

綠色 $y=xsin\phi $

藍色 $y=-xtan\theta tan\alpha $

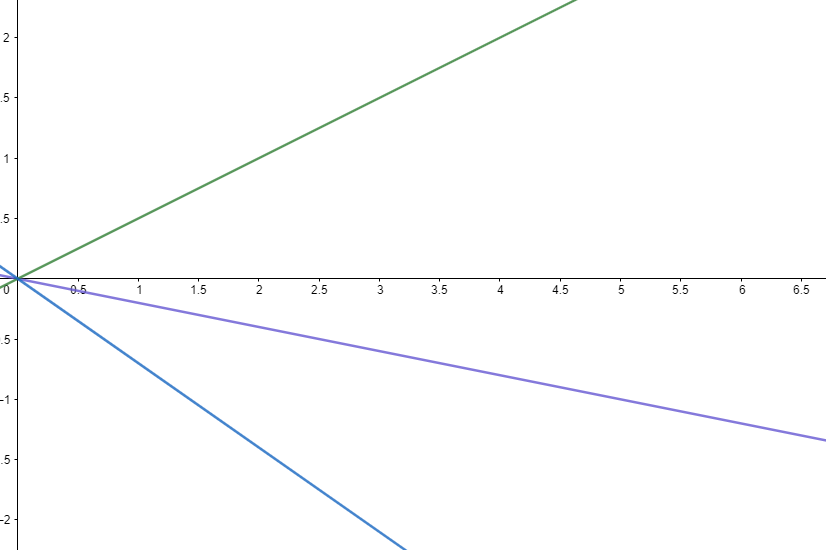紫色 $y=xsin\phi -xtan\theta tan\alpha $ 可以發現他就只是單調的遞減函數，也就是說雙錐會一路的往右邊滾過去而沒有來回的震盪現象了。

事實上在自然界很多有趣的現象都像$y=\frac{1}{x}$的雙錐一樣會在系統中震盪，而這也是科學精妙有趣的地方呢，你說是吧?